Unit 2!

 
On this page we will discuss if a specific function is a polynomial or not, what makes it a polynomial, how to write the function in standard form, finding the degree, the type, the leading coefficient, and end behavior.  
 

Step 1: Write the function

f(x) = 6x^3 -25x + 20; x = 5

Step 2: Determine if the funciton is a polynomial

 A function is a polynomial function if the degree of the exponents are positive whole numbers, if there is no square root, and if the function isnt being divided by x 

f(x) = 6x^3 -25x + 20; x = 5: this function in particular is a polynomial; given the previous rules

Step 3: Writing in standard form

To write a polynomial function in standard form, we must put our variables in order based on the degree

our function: f(x) = 6x^3 -25x + 20; x = 5, our function in standard form: f(x) = 6x^3 -25x^1 + 20x^0; x = 5

Step 4: Finding the Degree

The degree of our polynomial is determined by the biggest exponent in function

Degree of our function: 3, cubic

Step 5: Type of function

The type of function is determined by the degree of our function

Our degree: 3, so the type is cubic

degree   name

   1     linear (or monic)

   2     quadratic 

   3     cubic

   4     quartic 

   5     quintic

   6     hexic

   7     septic

   8     octic

   9     nonic 

  10     decic  

Step 6: Leading coefficient

This is pretty self explanitory, Leading coefficients are the numbers written in front of the variable with the largest exponent. Just like regular coefficients, they can be positive, negative, real, or imaginary as well as whole numbers, fractions or decimals. In our case the leading coefficient is 6

Step 7: End behavior

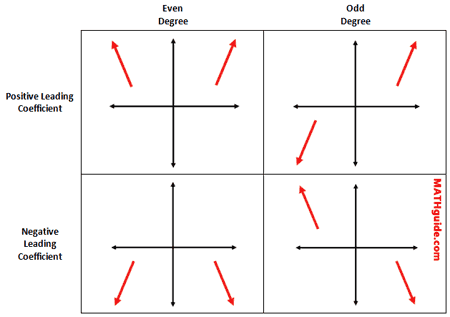
 given the information on this image, we know that the end behavior of our function is x - infinity, y + infinity, x + infinity, y + infinity.